Cálculo lógico
El cálculo lógico, o derivación lógica, es un algoritmo o sistema lógico que permite inferir o deducir un enunciado verdadero a partir de otro u otros que se tienen comoválidamente verdaderos.
La inferencia o deducción es una operación lógica que consiste en obtener un enunciado como -conclusión- a partir de otro(s) -premisa(s)- mediante la aplicación de reglas de inferencia.
Decimos que alguien infiere -o deduce- "T" de "R" si acepta que si "R" tiene valor de verdad V, entonces, necesariamente, "T" tiene valor de verdad V.
Las personas en nuestra tarea diaria, utilizamos constantemente el razonamiento deductivo; partimos de enunciados empíricos -supuestamente verdaderos y válidos- para concluir en otro enunciado que se deriva de aquellos.
La lógica matemática, como ciencia formal, se ocupa de analizar y sistematizar las reglas que permiten la transformación de unos enunciados -premisas- en otros -conclusiones- con objeto de convertir las operaciones deductivas en un cálculo riguroso y eficaz.
Al aplicar las reglas de este cálculo lógico a los enunciados que forman un argumento, previa la simbolización adecuada de los enunciados en fórmulas o Expresiones bien formadas (EBF)1 construimos un modelo dentro de un sistema deductivo que, referido al lenguaje ordinario, llamamos de Cálculo de deducción natural.
La representación gráfica de los símbolos (constantes lógicas) no está normalizada, lo que lleva a veces a ciertas dificultades de interpretación.
Sistematización de un cálculo[editar]
Reglas de formación de fórmulas[editar]
I.- Una letra enunciativa (con o sin subíndice) es una EBF (Expresión Bien Formada - en inglés wff o sea «well- formed formula» que significa «fórmula bien formada»).
II.- Si A es una fórmula, ¬ A también lo es.
III.- Si A es una EBF y B también, (A /\ B); (A \/ B); (A → B); (A ↔ B) también lo son.
IV.- Ninguna expresión es una fórmula del Cálculo sino en virtud de I, II, III.
Nota: A, B,... con mayúsculas están utilizadas como metalenguaje en el que cada variable expresa cualquier proposición, atómica o molecular.
Nota: Para la definición como función lógica de ¬, /\, \/, →, y ↔, véase Tabla de valores de verdad
Reglas de transformación
R.T.1: Dada una tesis EBF del cálculo, en la que aparecen variables de enunciados, el resultado de sustituir una, algunas o todas esas variables por expresiones bien formadas (EBF) del cálculo, será también una tesis EBF del cálculo. Y ello con una única restricción, si bien muy importante: cada variable ha de ser sustituida siempre que aparece y siempre por el mismo sustituto.
Veamos el ejemplo:
| 1 | ![\left [ \left ( p \land q \right ) \lor r \right ]\rightarrow t \lor s](http://upload.wikimedia.org/math/b/4/5/b45fe9c8e29197866d3b68f0abeb4de9.png) | Regla de Transformación |
| 2 |  | donde 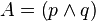 ; y donde ; y donde  |
| 3 |  | donde  |
O viceversa
| 1 |  | Regla de Transformación |
| 2 |  | donde  |
| 3 | ![\left [ \left ( p \land q \right ) \lor r \right ]\rightarrow t \lor s](http://upload.wikimedia.org/math/b/4/5/b45fe9c8e29197866d3b68f0abeb4de9.png) | donde  ; y donde ; y donde  |
Esta regla recibe el nombre de regla de sustitución
R.T.2: Si X es una tesis EBF del sistema y lo es también X --> Y, entonces Y es una tesis EBF del sistema.
Esta regla recibe el nombre de regla de separación
Sobre la base de estas dos reglas, siempre podremos reducir un argumento cualquiera a la forma:
[A /\ B /\ C...... /\ N ] ----> Y
lo que constituye un esquema de inferencia en el que de la verdad de las premisas A, B, N y su producto, podemos obtener la conclusión Y.
Concepto de modelo[editar]
Cuando en un Cálculo C, se establece una "correspondencia" de cada símbolo con elementos determinados individuales distinguibles entre sí, de un Universo L, real (tal universo L no es un conjunto vacío, por las mismas condiciones que hemos establecido), ENTONCES se dice que L es un MODELO de C.
El lenguaje natural como modelo de un cálculo lógico[editar]
Naturalmente el cálculo lógico es útil porque puede tener aplicaciones.
Pero ¿en qué consiste o cómo se hacen tales aplicaciones?
Para el cálculo de enunciados podemos considerar que el lenguaje natural es un modelo de C si podemos someterlo, es decir, aplicarle una correspondencia en C. Este proceso es lo que se llama formalización del lenguaje.
El lenguaje científico necesita "formalizar el lenguaje" a fin de evitar ambigüedades en las expresiones y en los contenidos semánticos de las palabras.
Cuando es posible se llega a una formalización completamente sometida a reglas previamente establecidas, como se pretende en este caso, y los elementos que constituyen las Expresiones bien formadas (EBF)s del lenguaje natural se pueden sustituir por variables sin significado, sin contenido semántico alguno porque realizarían la misma función que cualquier expresión de la lengua que cumpla la función sintáctica de la expresión. Entonces podemos proceder como en un cálculo.
No siempre es posible, pero es, sería, el lenguaje ideal de la ciencia,2 porque evitaría la necesidad de "interpretación". No habría más que sustiuir variables por variables lingüísticas y constantes por sus expresiones lingüísticas formalizadas.
Es lo que se pretende en este apartado: someter las expresiones del lenguaje natural a unas variables simbólicas mediante unas reglas de simbolización:
Reglas de simbolización[editar]
Regla I.
Cada uno de los enunciados simples del lenguaje natural se sustituirá por variables proposicionales simbolizadas por letras minúsculas: p, q, r, s, t,.....
Regla II.
Las expresiones del lenguaje natural tales como "no", "no es cierto", "no es el caso que" "es falso", "es imposible" y todas aquellas que sean equivalentes, se sustituirán por el símbolo de negación lógica: ¬
Llueve: p; No llueve: ¬ p
Regla III.
Las expresiones del lenguaje natural tales como "y", "ni", "pero", "que", "mas", y todas las que sean equivalentes, se sustituyen por el símbolo de conjunción lógica: ∧
Llueve: p; Hace frío: q; Llueve y hace frío: p ∧ q;
Regla IV.
Las expresiones del lenguaje natural tales como "o", "o...o", "bien...bien", "ya...ya", y sus equivalentes, se sustituyen por el símbolo de disyunción lógica: ∨
Llueve: p; Hace frío: q; O llueve o hace frío: p ∨ q
Regla V.
Las expresiones naturales tales como "si.... entonces", "luego...", "por tanto", "por consiguiente", "con tal que...", "se infiere", "se deduce" y sus equivalentes se sustituirán por el símbolo de implicación lógica o condicional material: →
Llueve: p; Hace frío: q; Si llueve entonces hace frío: p → q
Regla VI.
Las expresiones del lenguaje natural tales como "...si y solo si...", "...equivale a...", "...es igual a...", "vale por...", "...es lo mismo que...", y sus equivalentes se sustituirán por el símbolo bicondicional: ↔
Llueve: p; Hace frío: q; Llueve si y solo si hace frío: p ↔ q
Uso de paréntesis:
1.- No se utiliza paréntesis en aquellos casos en que los conectores afecten a enunciados simples o atómicos.
2.- Se utiliza paréntesis cuando el conector afecte a toda una conjunción, disyunción, condicional o bicondicional.
3.- Se utiliza el paréntesis en las expresiones conjuntivas y disyuntivas precedidas o seguidas de un condicionador o bicondicionador.
4.- Se utiliza el paréntesis en las expresiones que nos interese precisar la dominancia del conector, o bien porque los conectores posean la misma dominancia -como en el caso del conjuntor y del disyuntor que son idempotentes- o bien porque el sentido de la expresión exige la alteración de la dominancia de las conectivas fuertes -el condicionador y el bicondicionador que son las conectivas fuertes.
Cadena deductiva[editar]
Es una secuencia finita de enunciados de los cuales uno, la conclusión, se sigue necesariamente de los anteriores. Cada enunciado que forma parte de una determinada cadena deductiva constituye una línea de derivación.
- Las distintas líneas de derivación se colocarán una debajo de otra numeradas correlativamente a partir del uno.
- Las líneas correspondientes a las premisas iniciales irán provistas de un guion que precederá al número que tengan asignado.
- Si la línea corresponde a una fórmula inferida, se indicará a su derecha la regla aplicada y las premisas o las líneas a las que se ha aplicado la regla.
| Nº línea | EBF | Regla | Líneas |
| -1 | Premisa | ||
| -2 | Premisa | ||
| & | EBF | Regla S | línea €, 2 |
| $ | EBF | Regla R | línea 1 |
| n-2 | EBF | Regla X | líneas 1, $ |
| n-1 | EBF | Regla T | líneas 2, (n-2) |
| n | EBF | Regla U | líneas &, (n-1) |
| Cierre | Conclusión |
¿De qué manera puede obtenerse la conclusión?[editar]
a) La conclusión puede obtenerse "directamente" aplicando reglas de inferencia sobre las premisas iniciales.
b) Cuando en el desarrollo de la derivación es necesario utilizar premisas adicionales (supuestos no contemplados en las premisas dadas), decimos que la derivación es "subordinada", esto es, la obtención de la conclusión se subordina a la utilización de tales supuestos.
c) En caso de que la conclusión no pueda obtenerse por los métodos ya reseñados, recurriremos a la derivación "indirecta" o de "reducción al absurdo".
Observaciones técnicas
- Las líneas de derivación que introducen provisionalmente supuestos no contemplados en las premisas iniciales, deberán llevar una señal en escuadra mirando hacia abajo. El significado de la señal es: "supongamos por el momento..."
| Línea n | ┌ X | Significa que X es un supuesto provisional no contemplado en las premisas. |
| Línea n+1 | │ | Línea no utilizable fuera del supuesto. |
| Líneas | │ | Línea no utilizable fuera del supuesto. |
| línea n+a | └ Y | Significa el cierre del supuesto y su cancelanción |
- Los supuestos provisionales deberán ser cancelados antes de establecer la conclusión. Un supuesto provisional queda cancelado cuando, en una línea posterior de dicha derivación, se obtiene una fórmula tal que permite la deducción inmediata de otra fórmula que es independiente del referido supuesto. La cancelación de un supuesto se expresa cerrando la escuadra.
- La reducción al absurdo consiste en suponer como premisa provisional la negación de la fórmula que se pretende demostrar y obtener, mediante este supuesto, una contradicción. La consecuencia lógica será la negación del supuesto, es decir, la afirmación de la conclusión deseada.
- Todo supuesto provisional o las fórmulas de él derivadas incluidas dentro de las escuadras no podrán utilizarse después de la cancelación del supuesto como elementos de nuevas inferencias.
Reglas del cálculo de deducción natural. Cálculo proposicional[editar]
En este cálculo la proposición lógica es considerada como un todo en su condición de poder ser V, verdadera, o F, falsa.
Se distinguen las reglas primitivas y las derivadas. Las derivadas son producto de las primitivas, pero facilitan y reducen los pasos de la deducción. Asimismo las de reemplazo significan que una expresión puede ser sustituida directamente por su equivalente, a veces como definición.
Reglas primitivas[editar]
| Si dos gases tienen la misma temperatura entonces sus moléculas tienen el mismo promedio de energía cinética.
Volúmenes iguales de dos gases tienen el mismo número de moléculas.
Las presiones de dos gases son iguales si es el mismo su número de moléculas y sus energías cinéticas son iguales.
Por consiguiente si dos gases tienen la misma temperatura y el mismo volumen, tienen la misma presión.
Simbolización proposicional
Para dos gases:
t: Tener la misma temperatura.
c: Tener las moléculas la misma energía cinética.
v: Tener volúmenes iguales.
m: Tener igual número de moléculas.
p: Tener presiones iguales.
Esquema de inferencia, o argumento
t-->c /\ v-->m /\ (m/\c)-->p, |- (t/\v)-->p
Cálculo de Deducción
- 1 t--> c
- 2 v --> m
- 3 (m /\ c) --> p
┌ 4 t /\ v Supuesto
│ 5 t E.C.4
│ 6 v E.C.4
│ 7 c M.P.1,5
│ 8 m M.P.2,6
│ 9 m /\ c I.C.7,8
│ 10 c /\ m C.C.9
└ 11 p M.P.3-9
___________ Cierre supuesto
12 (t /\ v) --> p I.I.4-10
|
Las reglas primitivas son las siguientes:
Introducción del negador, demostración indirecta o absurdo I.N.
| ┌línea (n) | A | Supuesto provisional | |
| │ | - | Líneas derivadas provisionales | |
| │ | - | no utilizables fuera del supuesto | |
| └ línea (n+a) | B /\ ¬ B | Regla I.C, línea s, r | |
| _________ | Línea de cierre | ||
| Línea (n+a)+1 | ¬ A | Regla I.N. líneas (n - n+a+1) | Conclusión |
Eliminación del negador o Ex contradictione quodlibet ECQ
| línea n | A | Fórmula de la cadena | ||
| línea n+a | ¬A | Fórmula de la cadena | ||
| _______ | Línea de cierre | |||
| C | Regla E.N.,líneas n, n+a | Conclusión |
Resulta curiosa esta regla, pero es la que justifica argumentos tales como: "Si esto que dices es verdad, yo soy el Papa de Roma", que, son válidos aunque inútiles, pues se da por supuesta la falsedad de las premisas.
Por eso "ex contradictione quod libet", es decir, de una contradicción podemos concluir lo que queramos.
Introducción del conjuntor o producto: I.C.
| línea n | A | Fórmula de la cadena | ||
| línea n+a | B | Fórmula de la cadena | ||
| _______ | Cierre | |||
| A /\ B | Regla I.C., líneas n, n+a | Conclusión |
Eliminación del conjuntor o simplificación: E.C.
| línea n | A /\ B | |||
| _________ | Cierre | |||
| A | Regla E.C. línea n | Conclusión |
Introducción del disyuntor o adición: I.D.
| línea n | A | Fórmula de la cadena | |||
| _________ | Cierre | ||||
| A \/ B | Regla I.D., línea n | Conclusión |
Eliminación del disyuntor o casos: E.D.
| línea n | A \/ B | |
| ┌línea (n+1) | A | Supuesto provisional |
| │ | - | Líneas derivadas provisionales |
| │ | - | no utilizables fuera del supuesto |
| └ línea (n+ b) | C | Regla X, línea s, r |
| ┌línea (n+x) | B | Supuesto provisional |
| │ | - | Líneas derivadas provisionales |
| │ | - | no utillizables fuera del supuesto |
| └ línea (n+x)+a | C | Regla T, línea t, r |
| _________ | Cierre | |
| C | Casos,líneas [(n+1-n+b),(n+x-n+x+a)] |
Introducción del implicador o teoría de la deducción I.I.
| ┌línea (n) | A | Supuesto provisional |
| │ | - | Líneas derivadas provisionales |
| │ | - | no utilizables fuera del supuesto |
| └ línea (n+a) | B | Regla X, línea s, r |
| _________ | Cierre | |
| Línea (n+b)+1 | A → B | Regla I.I. líneas (n+1-n+b),conclusión |
Eliminación del implicador o Modus ponens E.I.
| línea n | A → B | Fórmula de la cadena | ||
| línea n+a | A | Fórmula de la cadena | ||
| _________ | Cierre | |||
| B | Regla E.I., líneas n, n+a | Conclusión |
No hay comentarios:
Publicar un comentario